728x90
반응형
SMALL
1. 단항(단일) 선형 회귀
- 한 개의 입력이 들어가서 한 개의 출력이 나오는 구조
# 패키지 불러오기
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 파이썬 코드를 재실행해도 같은 결과가 나올 수 있도록 random 시드를 설정
torch.manual_seed(10)
# 학습 데이터 설정
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[4],[6]])
print(x_train)
print(x_train.shape)
print(y_train)
print(y_train.shape)
>>>
tensor([[1.],
[2.],
[3.]])
torch.Size([3, 1])
tensor([[2.],
[4.],
[6.]])
torch.Size([3, 1])
# 데이터의 시각화
plt.figure(figsize=(8,5))
plt.scatter(x_train, y_train)
✅ 모델 정의
# 모델의 식 H = Wx + b
model = nn.Linear(1, 1) # 입력과 출력의 차원을 정의하는 선형 변환을 수행
print(model)
>>> Linear(in_features=1, out_features=1, bias=True)
✅ 모델의 학습 가능한 매개변수들을 리스트 형태로 출력'
print(list(model.parameters())) # 임의의 기울기와 bias
>>> [Parameter containing:
tensor([[-0.0838]], requires_grad=True), Parameter containing:
tensor([-0.0343], requires_grad=True)]
✅ 비용함수(Cost Function) 모델에 의한 예측값 도출
# 비용 함수
# Cost Function = Loss Function
y_pred = model(x_train)
print(y_pred)
>>>
tensor([[-0.1181],
[-0.2019],
[-0.2858]], grad_fn=<AddmmBackward0>)➡ 임의의 기울기와 bias값에 의한 이상한 결과가 나옴
✅ MSE 구하기
((y_pred - y_train) ** 2).mean()
>>> tensor(20.5513, grad_fn=<MeanBackward0>)✅ 예측값에 대한 추론
# 데이터 [[1],[2],[3]]
# W : [[-0.0838]], b: [-0.0343]
# pred: [[-0.1181], [-0.2019], [-0.2858]]
print(-0.0838*1 + -0.0343)
print(-0.0838*2 + -0.0343)
print(-0.0838*3 + -0.0343)
>>>
-0.1181
-0.2019
-0.28572. 경사하강법(Gradient Descent)
- 비용 함수의 값을 최소로 하는 W와 b를 찾는 알고리즘을 옵티마이저 알고리즘이라고 함
- 최적화 알고리즘이라고도 함
- 옵티마이저 알고리즘을 통해 W와 b를 찾아내는 과정을 '학습'이라고 부름
- 경사 하강법은 가장 기본적인 옵티마이저 알고리즘

# SGD(): 옵티마이저 알고리즘 중 하나
# 학습률(lr): 한 번 움직이는 거리(increment step)
optimizer = optim.SGD(model.parameters(), lr=0.01)
# loss 계산
loss = nn.MSELoss()(y_pred, y_train)
# gradient를 초기화: 기존의 grad값을 다시 초기화
optimizer.zero_grad()
# 비용함수를 미분하여 gradient(기울기)를 계산
# 역전파: 미분값을 정하고 방향을 찾은 다음에 주어진 lr만큼 이동하면서 얻은 기울기와 절편을 계산
loss.backward()
# W와 b를 업데이트
optimizer.step()
print(list(model.parameters()))
# W : [[-0.0838]], b: [-0.0343]
# W : [[0.1120]], b: [0.0498]
>>>
[Parameter containing:
tensor([[0.1120]], requires_grad=True), Parameter containing:
tensor([0.0498], requires_grad=True)]
# 학습(Training): 반복 훈련을 하면서 틀린 기울기(W)와 bias를 수정하여 오차를 계속 줄여나감
# epochs: 반복 훈련 횟수
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 100번마다 프린트
if epoch % 100 ==0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss: 6f}') # Loss값이 점점 작아짐 - 오차가 작아짐!
# 학습된 모델의 파라미터
print(list(model.parameters()))
# 결과값y = 1.9708 * x + 0.0663
>>>
[Parameter containing:
tensor([[1.9708]], requires_grad=True), Parameter containing:
tensor([0.0663], requires_grad=True)]
x_test = torch.FloatTensor([[10],[12.1234]])
y_pred = model(x_test)
print(y_pred)
>>> tensor([[19.7747],
[23.9595]], grad_fn=<AddmmBackward0>)
1.9708 * 10 + 0.0663
>>> 19.7743
1.9708 * 12.1234 + 0.0663
>>> 23.959096722. 다중 선형 회귀 실습
- 여러개의 입력이 들어가서 한 개의 출력이 나오는 구조
x_train = torch.FloatTensor([[73, 80, 85],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[76, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
print(x_train)
print(x_train.shape)
print(y_train)
print(y_train.shape)
>>>
tensor([[ 73., 80., 85.],
[ 93., 88., 93.],
[ 89., 91., 90.],
[ 96., 98., 100.],
[ 76., 66., 70.]])
torch.Size([5, 3])
tensor([[152.],
[185.],
[180.],
[196.],
[142.]])
torch.Size([5, 1])
# 가설: H = W1x1 + W2x2 + W3x3 + b
model = nn.Linear(3, 1) # 3개의 입력과 1개의 출력
print(model)
>>> Linear(in_features=3, out_features=1, bias=True)
print(list(model.parameters()))
>>> [Parameter containing:
tensor([[0.2238, 0.5419, 0.1360]], requires_grad=True), Parameter containing:
tensor([-0.1959], requires_grad=True)]- 임의의 W, b
- W: [[-0.2165, 0.1328, -0.3303]]
- b: [-0.1018]
optimizer = optim.SGD(model.parameters(), lr=0.000001) # 3개의 독립변수이기 때문에 lr의 소수점을 더 촘촘히 줌
# 학습
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f'Epoch {epoch}/{epoch} Loss: {loss: .6f}')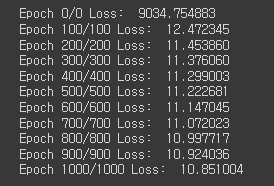
print(list(model.parameters()))
>>>[Parameter containing:
tensor([[0.6102, 0.8930, 0.4978]], requires_grad=True), Parameter containing:
tensor([-0.1918], requires_grad=True)]
x_test = torch.FloatTensor([[82, 92, 82]])
y_pred = model(x_test)
print(y_pred)
>>> tensor([[172.8189]], grad_fn=<AddmmBackward0>)3. 기온에 따른 지면 온도 예측 실습
📄 예제에 사용한 파일
import pandas as pd
import numpy as np
temp_df = pd.read_csv('/content/drive/MyDrive/KDT/Python/4.머신러닝 딥러닝/temps.csv', encoding='cp949')
temp_df
✅ 데이터 정보 보기
temp_df.info()
✅ 컬럼명 변경하기
temp_df.columns = [['location', 'location_name', 'date', 'temp', 'ground_temp']]
temp_df

✅ 결측지 확인하기
temp_df.isna().sum()
✅ 결측지 제거하기
temp_df.dropna(inplace=True)
✅ 수치형 데이터 확인하기
temp_df.describe()
✅ train data와 test data 나누기
x_data = temp_df[['temp']]
y_data = temp_df[['ground_temp']]
x_data = torch.FloatTensor(x_data.values) # ndarray로 변환: x_data.values
y_data = torch.FloatTensor(y_data.values)
print(x_data.shape)
print(y_data.shape)
# print(x_data.values)
>>> torch.Size([8779, 1])
torch.Size([8779, 1])
✅ 지면온도의 데이터보기
temp_df[['ground_temp']].values # 2차원 array
>>>
array([[-2.9],
[-2.4],
[-2.2],
...,
[-1.2],
[-1.5],
[-1.2]])
✅ 시각화 하여 보기
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5))
plt.scatter(x_data, y_data)
✅ 선형회귀 모델 설계, 최적의 optimizer 설정
model = nn.Linear(1, 1) # 1개의 input, 1개의 output
optimizer = torch.optim.SGD(model.parameters(), lr=0.001) # learning_rate=0.001
print(list(model.parameters()))
>>> [Parameter containing:
tensor([[-0.7576]], requires_grad=True), Parameter containing:
tensor([-0.9019], requires_grad=True)]✅ 모델에 데이터를 넣고 학습
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_data)
loss = nn.MSELoss()(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 100번마다 프린트
if epoch % 100 ==0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss: 6f}') # Loss값이 점점 작아짐 - 오차가 작아짐!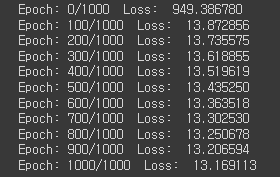
✅ 예측값 도출
y_pred = model(x_data).detach().numpy() # 텐서를 numpy 배열로 변환
y_pred
>>> array([[ -9.651394],
[ -8.082669],
[ -7.410358],
...,
[ -8.082669],
[ -9.987549],
[-10.211653]], dtype=float32)
✅ 실제값과 예측값을 시각화
plt.figure(figsize=(14, 8))
plt.scatter(x_data, y_data)
plt.scatter(x_data, y_pred)

728x90
반응형
LIST
'Python > ML&DL' 카테고리의 다른 글
| [파이썬, Python] 데이터로더(DataLoader) - 배치 단위로 학습시키기! (0) | 2023.06.29 |
|---|---|
| [파이썬, Python] 파이토치(Pytorch)로 논리 회귀(Logistic Regression)구현하기! (0) | 2023.06.26 |
| [파이썬, Python] 파이토치(Pytorch)란❓ & 파이토치의 특징 알아보기!🧐 (0) | 2023.06.23 |
| [파이썬, Python] 평가지표 - MSE, MAE, RMSE (0) | 2023.06.23 |
| [파이썬, Python] 머신러닝 - 7️⃣ KMeans (0) | 2023.06.19 |



