728x90
반응형
SMALL
1. 단항 논리 회귀 실습
- 논리 회귀(Logistic Regression)
- 분류를 할 때 사용하며 선형 회귀 공식으로부터 나왔기 때문에 논리 회귀라는 이름이 붙여짐
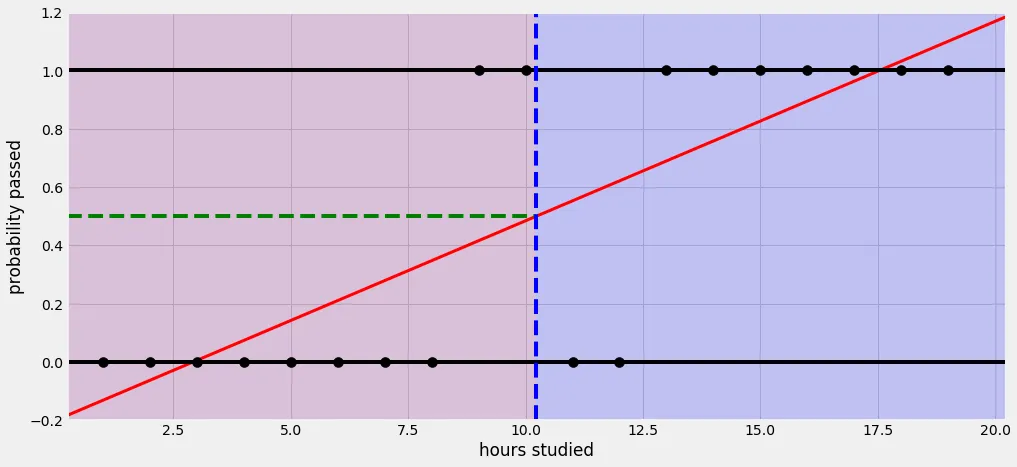

1-1. 시그모이드 함수
- 예측값이 0에서 1사이 값이 되도록 만듦
- 0에서 1사이의 연속된 값을 출력으로 하기 때문에 보통 0.5를 기준으로 구분

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 동일한 코드를 실행할 때마다 동일한 난수 시퀀스를 얻을 수 있도록 함
# 모델 초기화나 데이터 분할 등에서 난수를 사용하는 경우에 일관된 결과를 얻을 수 있음
torch.manual_seed(10)
x_train = torch.FloatTensor([[0], [1], [5], [9], [11], [15], [20]]) # 텐서형으로 데이터 생성
y_train = torch.FloatTensor([[0], [0], [0], [0], [1], [1], [1]]) # 11시간 공부한것부터 합격
print(x_train.shape, y_train.shape)
>>> torch.Size([7, 1]) torch.Size([7, 1])
plt.figure(figsize=(8,5))
plt.scatter(x_train, y_train)
# Sequential(): Pytorch에서 머신러닝/딥러닝 모델을 만들때 여러가지 레이어를 합칠 때 사용하는 메서드
model = nn.Sequential(
nn.Linear(1, 1), # 선형회귀
nn.Sigmoid() # 시그모이드 함수를 거쳐서
)
print(model)
>>> Sequential(
(0): Linear(in_features=1, out_features=1, bias=True)
(1): Sigmoid()
)
print(list(model.parameters())) # 임의의 값(학습 전)
>>> [Parameter containing:
tensor([[-0.0838]], requires_grad=True), Parameter containing:
tensor([-0.0343], requires_grad=True)]1-2. 비용 함수
- 논리 회귀에서는 nn.BCELoss() 함수를 사용하여 Loss를 계산
- BCE: Binary Cross Entropy

# 예측값
y_pred = model(x_train)
y_pred # 의미없는 결과(학습 전)
>>>
tensor([[0.4914],
[0.4705],
[0.3885],
[0.3124],
[0.2776],
[0.2156],
[0.1530]], grad_fn=<SigmoidBackward0>)
loss = nn.BCELoss()(y_pred, y_train)
loss
>>> tensor(0.9817, grad_fn=<BinaryCrossEntropyBackward0>)
# 옵티마이저 설정
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 학습
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.BCELoss()(y_pred, y_train)
optimizer.zero_grad() # 초기화
loss.backward() # 역전파
optimizer.step() # 업데이트
# 100번마다 프린트
if epoch % 100 ==0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss: 6f}')
# W, b 알아보기
print(list(model.parameters()))
>>>
[Parameter containing:
tensor([[0.2138]], requires_grad=True), Parameter containing:
tensor([-1.6024], requires_grad=True)]
# 2.5와 15.5의 테스트값으로 예측
x_test = torch.FloatTensor([[2.5], [15.5]])
y_pred = model(x_test)
print(y_pred)
>>> tensor([[0.2558],
[0.8470]], grad_fn=<SigmoidBackward0>)
# 임계치 설정하기
# 0.5 보다 크거나 같으면 1, 0.5보다 작으면 0
y_bool = (y_pred >= 0.5).float() # float형으로
print(y_bool) # 2.5는 0, 15.5는 1로 예측함
>>> tensor([[0.],
[1.]])2. 다항 논리 회귀 실습
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [0, 0, 0, 1, 1, 1, 2, 2] # 결과가 3개
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train) # Long형 Tensor
print(x_train.shape)
print(y_train.shape)
>>>
torch.Size([8, 4])
torch.Size([8])
# Sequential() : 하나의 레이어만 있어도 써주는것이 좋음!(순서 중요)
model = nn.Sequential(
nn.Linear(4,3) # 4개의 입력(독립변수), 3개의 출력
)
print(model)
>>> Sequential(
(0): Linear(in_features=4, out_features=3, bias=True)
)# 예측값
y_pred = model(x_train)
print(y_pred)
>>>
tensor([[-0.1358, 1.5655, -0.0104],
[-1.0986, 1.3559, 0.5590],
[-1.4625, 1.2105, 0.7214],
[-2.3103, 1.4702, 1.2348],
[-1.0576, 3.7047, 0.7548],
[-1.7209, 1.1885, 1.0922],
[-1.5469, 3.1835, 1.0722],
[-1.8061, 3.6010, 1.2775]], grad_fn=<AddmmBackward0>)
- 다항 논리 회귀에서는 BCELoss() 함수 대신에 CrossEntropyLoss() 함수를 사용
- CrossEntropyLoss(): softmax 함수가 포함되어있음
- softmax 함수: 클래스의 개수만큼 확률을 반환(0일 확률, 1일 확률, 2일 확률)
loss = nn.CrossEntropyLoss()(y_pred, y_train)
print(loss)
>>> tensor(1.7613, grad_fn=<NllLossBackward0>)
✅ 학습
optimizer = optim.SGD(model.parameters(), lr=0.1)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.CrossEntropyLoss()(y_pred, y_train) # softmax 포함, 내부적으로 원핫인코딩 -> 각각의 확률 반환
optimizer.zero_grad() # 초기화
loss.backward() # 역전파
optimizer.step() # 업데이트
# 100번마다 프린트
if epoch % 100 ==0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss: 6f}')
✅ test 값으로 확인
x_test = torch.FloatTensor([[1,2,5,6]])
y_pred = model(x_test)
y_pred
>>>
tensor([[-4.9985, 3.4779, 2.0804]], grad_fn=<AddmmBackward0>)
✅ 예측값과 확률 구하기
y_prob = nn.Softmax(1)(y_pred) # 1차원 데이터를 넣음
y_prob
>>> tensor([[1.6701e-04, 8.0166e-01, 1.9817e-01]], grad_fn=<SoftmaxBackward0>)
print(f'0일 확률: {y_prob[0][0]:.2f}')
print(f'1일 확률: {y_prob[0][1]:.2f}')
print(f'2일 확률: {y_prob[0][2]:.2f}')
>>>
0일 확률: 0.00
1일 확률: 0.80
2일 확률: 0.20
# argmax: y_prob에서 가장 큰 값의 인덱스를 반환하는 연산
# axis=1 매개변수는 텐서의 두 번째 차원을 따라 연산을 수행하라는 것
torch.argmax(y_prob, axis=1)
>>> tensor([1]) # 1로 예측함3. 경사 하강법(Gradient Descent)
- 주어진 손실 함수(Loss Function)를 최소화하기 위해 사용되며, 모델의 가중치와 편향을 업데이트하는 방법
3-1. 배치 사이즈(Batch Size)
- 배치 사이즈(batch size)는 경사 하강법 알고리즘에서 한 번의 파라미터 업데이트를 위해 사용되는 학습 데이터의 샘플 개수
- 즉, 학습 데이터를 작은 묶음(batch)으로 나누어서 모델을 학습하는 방법
- 일반적으로 배치 사이즈는 하이퍼파라미터로 설정되며, 선택하는 방법은 다양
- 작은 배치 사이즈는 메모리 사용량이 적고 계산 효율성이 높지만, 노이즈가 많을 수 있음
- 큰 배치 사이즈는 메모리 사용량이 늘어나고 계산 효율성이 감소하지만, 더 안정적인 그래디언트 추정치를 얻을 수 있음
3-2. 배치 경사 하강법(Vanilla Gradient Descent)
- 가장 기본적인 경사 하강법
- 데이터셋 전체를 고려하여 손실함수를 계산
- 한 번의 Epoch에 모든 파라미터 업데이트를 단 한번만 수행
- Batch의 개수와 Iteraion은 1이고 Batch size는 전체 데이터의 개수
- 파라미터 업데이트 할 때 한 번에 전체 데이터셋을 고려하기 때문에 모델 학습 시 많은 시간과 메모리가 필요하다는 단점
3-3. 확률적 경사 하강법(SGD, Stochastic Gredient Descent)
- 확률적 경사 하강법(SGD, Stochastic Gredient Descent)은 배치 경사 하강법이 모델 학습 시 많은 시간과 메모리가 필요하다는 단점을 개선하기 위해 제안된 기법
- Batch size를 1로 설정하고 파라미터를 업데이트 하기 때문에 배치 경사 하강법보다 훨씬 빠르고 적은 메모리로 학습이 진행
- 파라미터 값의 업데이트 폭이 불안정하기 때문에 정확도가 낮은 경우가 생길 수 있음

3-4. 미니 배치 경사 하강법(Mini-batch Gradient Descent)
- 미니 배치 경사하강법(Mini-batch Gradient Descent)은 Batch size가 1도 전체 데이터 개수도 아닌 경우
- 배치 경사 하강법보다 모델 학습 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있음
- 딥러닝 분야에서 가장 많이 활용되는 경사 하강법
- 일반적으로 Batch size를 32, 64, 128과 같이 2의 n제곱에 해당하는 값으로 사용하는게 보편적 (CPU 내부 설계 자체가 2의 n제곱 연산이 가장 속도가 빠르기 때문에
4. 경사하강법의 여러가지 기술들
4-1. 확률적 경사 하강법(SGD)
- 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법
4-2. 모멘텀(Momentum)
- 관성이라는 물리학의 법칙을 응용한 방법
- 경사 하강법에 관성을 더 해줌
- 접선의 기울기에 한 시점 이전의 접선의 기울기 값을 일정한 비율만큼 반영
- 언덕에서 공이 내려올 때 중간의 작은 웅덩이에 빠지더라도 관성의 힘으로 넘어서는 효과를 줄 수 있음
local minimum에서 빠져나올 수 있도록 함

4-3. 아다그라드(Adagrad)
- 모든 매개변수에 동일한 학습률(learning rate)을 적용하는 것은 비효율적이라는 생각에서 만들어진 학습 방법
- AdaGrad는 Feature별로 학습률(Learning rate)을 Adaptive하게, 즉 다르게 조절하는 것이 특징
- 처음에는 크게 학습하다가 작게 학습시킴
4-4. 아담(Adam)
- 아다그라드 + 모멘텀
- 학습의 방향과 크기(=Learning rate)를 모두 개선한 기법으로 딥러닝에서 가장 많이 사용되어오던 최적화 기법
- 여러 기술들이 합쳐졌기 때문에 속도가 느릴 수 있음
# Adam으로 바꿔서 다시 학습 - Accuracy가 매우 좋아짐!
model = nn.Sequential(
nn.Linear(13, 3)
)
optimizer = optim.Adam(model.parameters(), lr=0.01)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.CrossEntropyLoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_prob = nn.Softmax(1)(y_pred) # 클래스별 확률을 반환(차원을 1)
y_pred_index = torch.argmax(y_prob, axis=1) # 각 샘플별로 클래스별 확률 중 가장 큰값을 가지는 클래스의 인덱스값(axis=1:각 행에서)
y_train_index = torch.argmax(y_train, axis=1) # 실제 클래스 레이블에서 각 샘플별로 가장 큰 값을 가지는 클래스의 인덱스(axis=1: 각 행에서)
accuracy = (y_train_index == y_pred_index).float().sum() / len(y_train) * 100 # bool값으로 반환된 데이터를 float으로 형변환 후 더함
print(f'Epoch { epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
y_pred = model(x_test)
y_pred[:5]
>>> tensor([[38.3035, 41.4661, 36.4269],
[23.5532, 30.4381, 23.5679],
[48.5956, 47.4519, 42.9946],
[29.9729, 36.5060, 29.0688],
[65.1588, 60.0035, 59.2508]], grad_fn=<SliceBackward0>)
y_prob = nn.Softmax(1)(y_pred)
y_prob[:5] # 예측값에 대한 확률
>>> tensor([[4.0348e-02, 9.5347e-01, 6.1778e-03],
[1.0210e-03, 9.9794e-01, 1.0361e-03],
[7.5624e-01, 2.4096e-01, 2.7938e-03],
[1.4515e-03, 9.9796e-01, 5.8772e-04],
[9.9158e-01, 5.7203e-03, 2.6948e-03]], grad_fn=<SliceBackward0>)
print(f'0번 품종일 확률: {y_prob[0][0]: .2f}')
print(f'1번 품종일 확률: {y_prob[0][1]: .2f}')
print(f'2번 품종일 확률: {y_prob[0][2]: .2f}')
>>>
0번 품종일 확률: 0.04
1번 품종일 확률: 0.95
2번 품종일 확률: 0.01
y_pred_index = torch.argmax(y_prob, axis=1)
y_test_index = torch.argmax(y_test, axis=1) # 예측된 레이블에서 각 샘플별로 가장 큰 값을 가지는 클래스의 인덱스(axis=1: 각 행에서)
accuracy = (y_test_index == y_pred_index).float().sum() / len(y_test) * 100
print(f'테스트 정확도는 {accuracy:.2f}% 입니다')
>>> 테스트 정확도는 88.89% 입니다

728x90
반응형
LIST
'Python > ML&DL' 카테고리의 다른 글
| [파이썬, Python] 딥러닝(DeepLearning) - 퍼셉트론과 역전파 (0) | 2023.06.29 |
|---|---|
| [파이썬, Python] 데이터로더(DataLoader) - 배치 단위로 학습시키기! (0) | 2023.06.29 |
| [파이썬, Python] 파이토치(Pytorch)로 선형회귀(Linear Regression) 구현하기! (0) | 2023.06.23 |
| [파이썬, Python] 파이토치(Pytorch)란❓ & 파이토치의 특징 알아보기!🧐 (0) | 2023.06.23 |
| [파이썬, Python] 평가지표 - MSE, MAE, RMSE (0) | 2023.06.23 |



